贪心算法

发表于

1. 介绍

1、最自然智慧的算法

2、用一种局部最功利的标准，总是能做出在当前看来是最好的选择

3、难点在于证明局部最优解可以最终得到全局最优解

4、对于贪心算法的学习主要是以经验为主，尝试为主

1.1 举例

正例：假设一个数组中N个正数，第一个挑选出来的数乘以1，第二个挑选出来的数乘以2……第N次挑选出来的数乘以N，总的加起来是我们的分数。怎么挑选数字使我们达到最大分数？

解答：数组按从小到大的顺序排序，我们按顺序依次挑选，最终结果就是最大的。本质思想是因子随着挑选次数的增加会增大，我们尽量让大数去结合大的因子。

贪心算法有时是无效的，下文会举贪心算法无效的例子

反例：在下面的矩阵中，先从左上走到右下，再从右下回到左上，每个1只能拿到一次，要求拿到最多数量的1

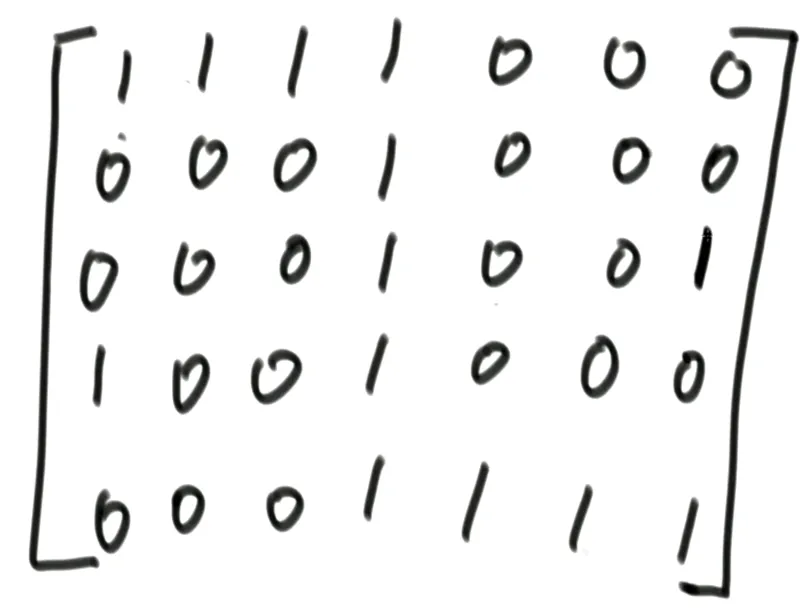
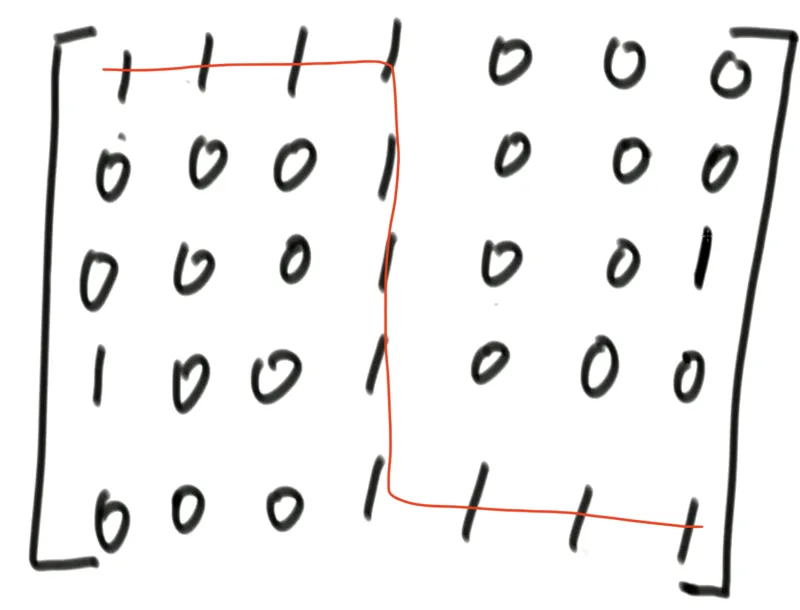
如果是贪心，从左上走到右下的时候会尽量多拿1，也就是走出如下路线，但是结果是还剩两个1就无法全部拿到了：

但其实本题有方法拿到全部的1：

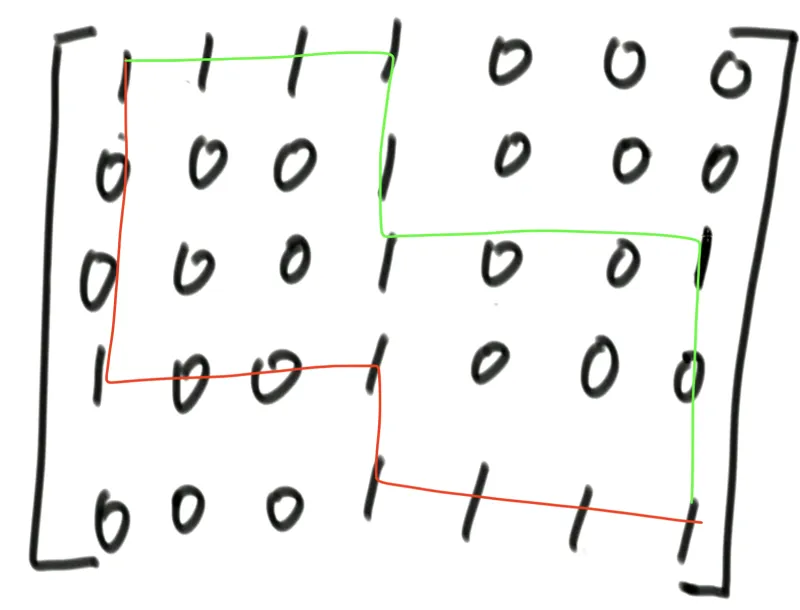
此时贪心策略就是失败了。要用动态规划。

1.2 字典序问题

题目：给定一个由字符串组成的数组 strs，必须把所有的字符串拼接起来，返回所有可能的拼接结果中，字典序最小的结果。

字典序直观理解，两个单词放到字典中，从头开始查找这个单词，哪个先被查找到，哪个字典序小。

字典序严格定义，我们把字符串当成 K 进制的数，a-z 当成 26 进制的正数，

  1. 如果字符长度一样，abk > abc，那么我们说 abk的字典序更大。

  2. 字符长度不一样，例如 ac 和 b，那么我们要把短的用 0 补齐，0 的字典序小于 a，那么 ac<b0，高位 b>a 即可比较出来 ac<b。

贪心策略1：按照单个元素字典序贪心，例如在[ac,bk,sc,ket]字符串数组中，我们拼接出来最终的字符串字典序最小，那么我们依次挑选字典序最小的进行拼接。得到acbkketsc。

但是这样的贪心不一定是正确的，例如[ba,b]按照上述思路的贪心结果是bba，但是bab明显是最小的结果

贪心策略2：两个元素x和y，x拼接y小于等于y拼接x，那么x放前，否则y放前面。例如 x=b,y=ba。bba大于bab 的字典序，那么ba放前面。

问题是，上面的比较排序策略有没有传递性呢？如果没有传递性，那这个策略就是无效的。

证明：

我们把拼接当成k进制数的数学运算，把a-z的数当成26进制的数，ks拼接ts实质是

先证明我们比较的传递性：证明对任意字符串来说，a拼接b小于b拼接a，b拼接c小于等于c拼接b，则推导出a拼接c小于等于c拼接a。

a拼接b等于 。设 ，所以我们的两个条件就为：

一式两边同时 得到：

二式两边同时 得到：

因此有相同的部分 ，得到：

也就是a拼c的字典序小于c拼a。

至此，我们证明出我们的排序具有传递性质。

根据我们排序策略得到的一组序列，证明我们任意交换两个字符的位置，都会得到更大的字典序。

例如按照策略二得到的amnb序列，我们先把 a 和 m 交换，由于按照策略二得到的序列，满足 a.m <= m.a ，所以manb > amnb，同理 mnab > manb，mnba > mnab，mbna > mnba bmna > mbna，根据传递性，得到 amnb < bmna。那么最终数学归纳法，得到策略二的正确性。

所以贪心算法的证明实质是比较复杂的，我们大可不必每次去证明贪心的正确性.

1
2
3
4
5
6
7
def min_dictionary_order(strs):
    n = len(strs)
    for i in range(n - 1, 0, -1):
        for j in range(i):
            if strs[j] + strs[j + 1] > strs[j + 1] + strs[j]:
                strs[j], strs[j + 1] = strs[j + 1], strs[j]
    return "".join(strs)

2. 贪心求解

2.1 标准过程

1、分析业务

2、根据业务逻辑找到不同的贪心策略

3、对于能举出反例的策略，直接跳过，不能举出反例的策略要证明有效性，这往往是比较困难的，要求数学能力很高且不具有统一的技巧性

2.2 实际解题套路

1、实现一个不依靠贪心策略的解法X，可以用暴力尝试

2、脑补出贪心策略A，贪心策略B，贪心策略C……

3、用解法X和对数器，用实验的方式得知哪个贪心策略正确

4、不要去纠结贪心策略的证明

贪心类的题目在笔试中，出现的概率高达6到7成，而面试中出现贪心的概率不到2成。因为笔试要的是淘汰率，面试要的是区分度。由于贪心的解决完全取决于贪心策略有没有想对，有很高的淘汰率但是没有很好的区分度

3. 例题

最大参会数量

一些项目要占用一个会议室宣讲，会议室不能同时容纳两个项目宣讲。给你每个项目的开始时间和结束时间，你来安排宣讲的日程，要求会议室进行宣讲的场数最多。返回最多的宣讲场次。

思路：本题常见的几种贪心策略，一种是按照谁先开始安排谁，第二种按照持续时间短的先安排，第三种按照谁先结束安排谁。

通过验证，无需证明得出第三种贪心策略是正确的。

可以设计一个会议的类：

1
2
3
4
class Program:
    def __init__(self, start, end):
        self.start = start
        self.end = end

暴力的解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def violence(programs: List[Program]) -> int:
    if not programs or len(programs) == 0:
        return 0
    return process_violence(programs, 0, 0)


def process_violence(programs, arranged, cur_time):
    """
    :param programs: 剩下没有安排的会议
    :param arranged: 已经安排了多少会议的数量
    :param cur_time: 目前来到的时间点
    :return: 最大的安排会议的数量
    """
    if len(programs) == 0:
        return arranged
    max_num = arranged
    # 当前安排的会议是什么会，每一个都枚举
    for i in range(len(programs)):
        if programs[i].start >= cur_time:
            next = programs[:i] + programs[i + 1:]
            max_num = max(max_num, process_violence(next, arranged + 1, programs[i].end))
    return max_num

贪心解法：

1
2
3
4
5
6
7
8
9
def greedy(programs):
    programs.sort(key=lambda x: x.end)
    cur_time = 0
    res = 0
    for i in range(len(programs)):
        if cur_time <= programs[i].start:
            res += 1
            cur_time = programs[i].end
    return res

随机生成一个待选会议的列表：

1
2
3
4
5
6
7
8
9
10
def generate_programs(program_size, time_max):
    ans = []
    for _ in range(random.randint(10, program_size)):
        r1 = random.randint(0, time_max)
        r2 = random.randint(0, time_max)
        if r1 == r2:
            ans.append(Program(r1, r1 + 1))
        else:
            ans.append(Program(min(r1, r2), max(r1, r2)))
    return ans

进行两种方法的比较，可以发现运行多次，我们的贪心策略都是正确的：

1
2
3
4
5
6
7
if __name__ == '__main__':
    program_size = 100
    time_max = 50
    programs = generate_programs(program_size, time_max)
    ground_truth = violence(programs)
    ans = greedy(programs)
    print(ground_truth, ans)

居民楼照明问题

给定一个字符串 str ，只由 X 和 . 两种字符构成。X 表示墙，不能放灯，也不需要点亮，. 表示居民点，可以放灯，需要点亮。

如果灯放在 i 位置，可以让 i-1，i 和 i+1 三个位置被点亮，返回如果点亮所有居民点，至少需要几盏灯？

例如： X..X......X..X. 需要至少5盏灯。

暴力法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def violence(road):
    if not road:
        return 0
    return process(list(road), 0, set())


def process(road, index, lights):
    """
    遍历所有能照亮.的方案，且在这些方案中，最少需要多少灯
    :param road: 路的字符串
    :param index: 当前位置
    :param lights: 安排了灯的位置，记录为road字符串的下标
    :return:
    """
    if index == len(road):
        for i in range(len(road)):  # 本轮遍历结束了
            if road[i] == '.':
                # 灯无法照亮所有居民区，返回
                if (i - 1) not in lights and i not in lights and (i + 1) not in lights:
                    return float('inf')
        return len(lights)
    else:
        no = process(road, index + 1, lights)  # 当前位置不放灯的情况
        yes = float('inf')  # 当前位置放灯的情况（需要当前位置是.）
        if road[index] == '.':
            lights.add(index)
            yes = process(road, index + 1, lights)
            lights.remove(index)  # 这里要回溯恢复现场
        return min(no, yes)

贪心策略：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def greedy(road):
    index = 0
    light = 0
    while index < len(road):
        if road[index] == 'X':
            index += 1
        else:  # idx位置是.
            light += 1  # 不管怎么样会放一盏灯，具体放哪里是下面讨论的
            if index + 1 == len(road):  # 此时我把灯放在idx位置，且流程结束了
                break
            else:
                if road[index + 1]=='X': # 此时把灯放在idx位置，所以直接跳到idx+2位置
                    index += 2
                else:  # 此时我把灯放在idx+1位置，所以直接跳到idx+3位置
                    index += 3
    return light

哈夫曼树问题

一根金条切成两半，是需要花费和长度值一样的铜板的。比如长度为20的金条，不管怎么切，都需要花费20个铜板。一群人想整分整块金条，怎么分最省铜板？

例如：给定数组 [10,20,30]，代表一共三个人，整块金条长度为60，金条要分成10,20,30三个部分。

  • 如果先把长度为60的金条分成10和50，花费60；再把长度为50的金条分成20和30，花费50；一共需要花费110个铜板。

  • 但是如果先把长度为60的金条分成30和30，花费60;再把30的金条分成10和20,花费30；一共花费90个铜板。

输入一个数组，返回分割的最小代价。

思路：就是每次选择两个最小的出堆，然后相加后回到堆。

1
2
3
4
5
6
7
8
9
10
def greedy(arr):
    heap = []
    for elem in arr:
        heapq.heappush(heap, elem)
    sum, cur = 0, 0
    while len(heap) > 1:  # 弹出两个最小的，相加后放回堆中
        cur = heapq.heappop(heap) + heapq.heappop(heap)
        sum += cur
        heapq.heappush(heap, cur)
    return sum

项目花费和利润问题

输入：正数数组 costs，正数数组 profits ,正数 K ,正数 W

costs[i] 表示 i 号项目的花费，profits[i] 表示 i 号项目在扣除花费之后还能挣到的钱（利润）

K表示你只能最多做K个项目，W表示你的初始资金。

说明：每做完一个项目，马上获得收益，可以支持你去做下一个项目。不能并行做项目。

输出：你最后获得的最大钱数。

思路：贪心策略，首先需要求出当前的资金能够解锁的全部项目。项目可以根据项目花费放入一个小根堆，依次用 W 比较堆顶然后出堆。有了所有的解锁项目，那么，既然追求最大利润，就把解锁的全部项目根据利润放入大根堆，然后每次出堆最大利润的项目来做就可以了。

这里因为涉及小根堆和大根堆，需要定义不同的比较器，所以用Java实现比较方便

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int findMaximizedCapital(int k, int w, int[] profits, int[] capital) {
    int n = profits.length;
    // 根据成本建立小根堆
    PriorityQueue<int[]> minCost = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
    for (int i = 0; i < n; i++) {
        minCost.offer(new int[]{capital[i], profits[i]});
    }
    // 根据利润建立大根堆
    PriorityQueue<int[]> maxProfit = new PriorityQueue<>((a, b) -> b[1] - a[1]);
    for (int i = 0; i < k; i++) {
        // 现有的本钱w可以进行哪些项目，这些项目全部进大根堆
        while (!minCost.isEmpty() && minCost.peek()[0] <= w) {
            maxProfit.offer(minCost.poll());
        }
        if (maxProfit.isEmpty()) {
            return w;
        }
        w += maxProfit.poll()[1]; // 直接获得最大利润项目的利润
    }
    return w;
}