归并排序与快速排序

发表于 更新于

1. 归并排序

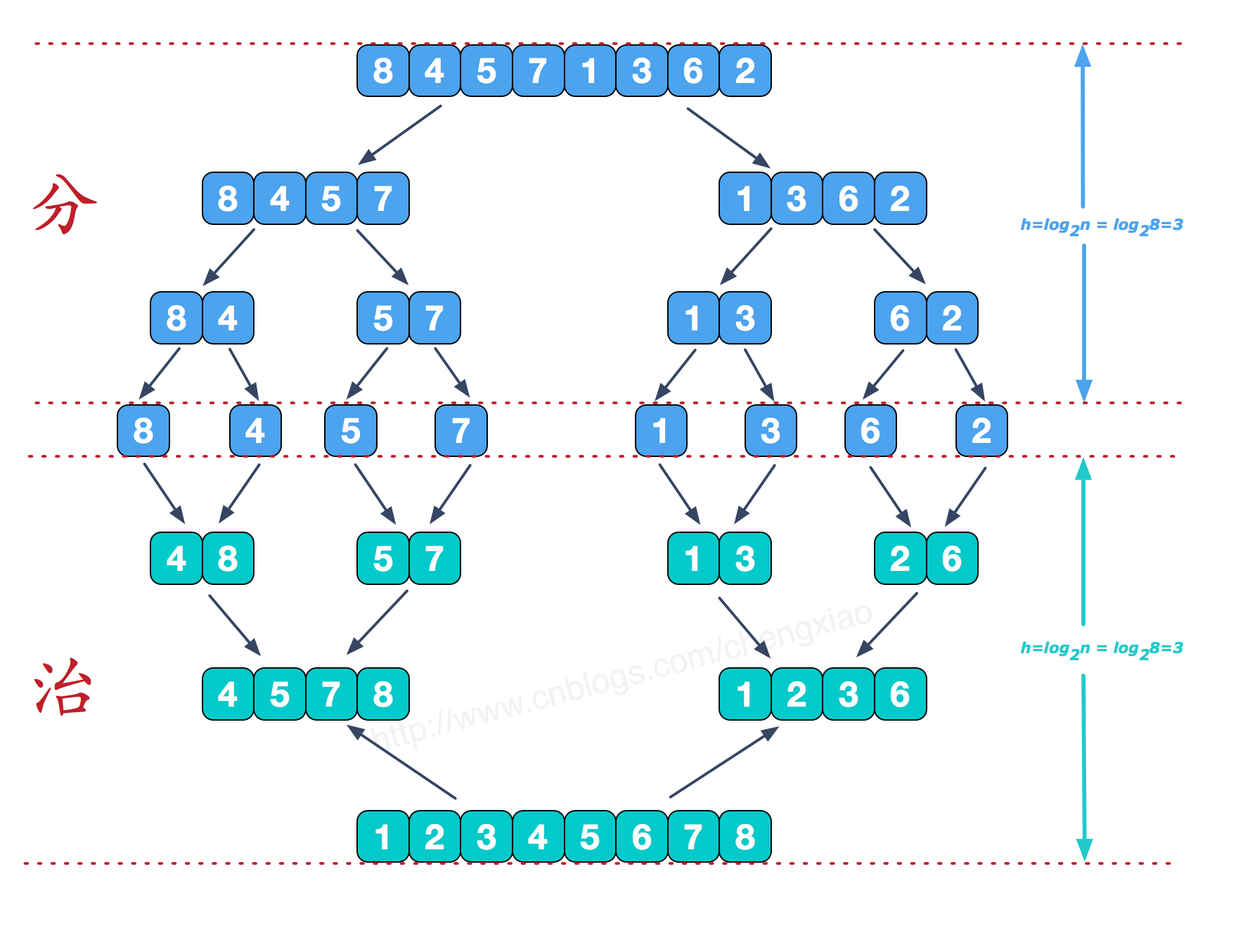
归并排序（Merge Sort）是一种基于分治思想的稳定排序算法。它将一个待排序的数组递归地分成两个子数组，分别对这两个子数组进行排序，然后再将排好序的子数组合并成一个有序的数组。

一般有两种写法，递归的和非递归的。

1.1. 递归版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
 public static void mergeSortRecursive(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    processRecursive(arr, 0, arr.length - 1);
}

private static void processRecursive(int[] arr, int left, int right) {
    if (left == right) {
        return;
    }
    int mid = left + ((right - left) >> 1);
    processRecursive(arr, left, mid);
    processRecursive(arr, mid + 1, right);
    mergeBoth(arr, left, mid, right);
}

private static void mergeBoth(int[] arr, int left, int mid, int right) {
    int[] help = new int[right - left + 1];
    int p = left;
    int q = mid + 1;
    int index = 0;
    while (p <= mid && q <= right) {
        if (arr[p] <= arr[q]) {
            help[index++] = arr[p++];
        } else {
            help[index++] = arr[q++];
        }
    }
    while (p <= mid) {
        help[index++] = arr[p++];
    }
    while (q <= right) {
        help[index++] = arr[q++];
    }
    for (int i = 0; i < help.length; i++) {
        arr[left + i] = help[i];
    }
}

1.2. 非递归版本

非递归的归并，基本思想是：从 merge_size = 1 开始，从一个数组的开头开始遍历，每次选择 merge_size 个元素作为左组，再选 merge_size 个作为右组，然后左右两组合并，直到我无法找到足够元素形成两个组为止。然后，merge_size 扩大一倍，继续从头开始遍历……直到 merge_size 超过数组长度，算法结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public static void mergerSortUnrecursive(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    int mergeSize = 1;
    int n = arr.length;
    while (mergeSize < n) {
        int left = 0;
        while (left < n) {
            int mid = left + mergeSize - 1;
            if (mid >= n) { // 无法再划出右半边了
                break;
            }
            int right = Math.min(mid + mergeSize, n - 1);
            mergeBoth(arr, left, mid, right);
            left = right + 1;
        }
        mergeSize<<=1;
    }
}

// 这个函数和上面的一样
private static void mergeBoth(int[] arr, int left, int mid, int right) {
    int[] help = new int[right - left + 1];
    int p = left;
    int q = mid + 1;
    int index = 0;
    while (p <= mid && q <= right) {
        if (arr[p] <= arr[q]) {
            help[index++] = arr[p++];
        } else {
            help[index++] = arr[q++];
        }
    }
    while (p <= mid) {
        help[index++] = arr[p++];
    }
    while (q <= right) {
        help[index++] = arr[q++];
    }
    for (int i = 0; i < help.length; i++) {
        arr[left + i] = help[i];
    }
}

归并排序无论递归还是非递归形式，其复杂度都是$O(nlogn)$，它比那些复杂度是 $O(n^2)$ 的排序算法要更加优秀，原因是归并排序没有浪费比较行为，每次都将之前的比较行为保存了下来（元素在左右两组组内的相对位置被保存下来了，不会再变了)，达到了较高的效率。但比如说，选择排序，每一轮让所有数比较一遍，最终只是确定了一个数的位置，有大量比较的行为被浪费。

1.3. 数的小和（归并思想）

在一个数组中，一个数左边比它小的数的总和，叫数的小和，所有数的小和累加起来，叫数组小和，求数组小和。

例如，[1,3,4,2,5]，其小和为：1+1+3+1+1+3+4+2=16

思路：还是归并的那一套流程，在合并（merge_both）的时候，

  • 如果左组的数（记为a）小于右组的数，那就产生小和，若右组有x个元素大于a，则产生小和，为 x*a；

  • 如果左组的数和右组相等，那就先拷贝右组的数，且不产生小和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public static int smallSum(int[] arr) {
    if (arr == null || arr.length < 2) {
        return 0;
    }
    return process(arr, 0, arr.length - 1);
}
private static int process(int[] arr, int left, int right) {
    if (left == right) {
        return 0;
    }
    int mid = left + ((right - left) >> 1);
    return process(arr, left, mid)
    + process(arr, mid + 1, right)
    + mergeBoth(arr, left, mid, right);
}
private static int mergeBoth(int[] arr, int left, int mid, int right) {
    int[] help = new int[right - left + 1];
    int p = left;
    int q = mid + 1;
    int cur = 0;
    int res = 0;
    while (p <= mid && q <= right) {
        // 对于arr[p]来说，arr[q]之后所有的值都比它大，故都要记入小和结果中
        if (arr[p] < arr[q]) {
            res += arr[p] * (right - q + 1);
            help[cur++] = arr[p++];
        } else {
            help[cur++] = arr[q++];
        }
    }
    while (p <= mid) {
        help[cur++] = arr[p++];
    }
    while (q <= right) {
        help[cur++] = arr[q++];
    }
    for (int i = 0; i < help.length; i++) {
        arr[left + i] = help[i];
    }
    return res;
}

举一反三，如果要求数组中右边有多少更小的元素，也就是求数组逆序对的问题，那也可以套用这个归并排序的模板

2. 快速排序

2.1. 荷兰国旗问题

给定一个数组，和一个目标值 num，把数组中小于 num 的放在左边，大于 num 的放在右边，其他等于 num 的放在中间。

思路：维护两个区，一个是小于区，一个是大于区，小于区往右侧扩张，大于区往左侧扩张，然后扫描一遍数组，当前位置记为 i

  • 如果扫描的当前值等于 num，那么什么也不做，i 跳下一个位置

  • 如果扫描的当前值小于 num，那当前值和小于区下一个（右边的一个）元素交换，小于区扩大一位，i跳下一个位置

  • 如果扫描的当前值大于 num，那当前值和大于区上一个（左边的一个）元素交换，大于区扩大一位，i停在原地（不跳下一个位置）

2.2. 随机快排

之后再来看快排算法，随机选择pivot值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public static void quickSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    process(arr, 0, arr.length - 1);
}

private static void process(int[] arr, int left, int right) {
    if (left >= right) {
        return;
    }
    Random random = new Random();
    int randLoc = random.nextInt((right - left) + 1) + left;
    swap(arr, randLoc, right);
    int[] midArea = partition(arr, left, right);
    process(arr, left, midArea[0] - 1);
    process(arr, midArea[1] + 1, right);
}

private static int[] partition(int[] arr, int left, int right) {
    if (left > right) {
        return new int[]{-1, -1};
    }
    if (left == right) {
        return new int[]{left, right};
    }
    int pivot = arr[right];
    int less = left - 1;  // 小于pivot值的区域
    int more = right;   // 大于pivot值的区域
    int cur = left;
    while (cur < more) {
        if (arr[cur] == pivot) {
            cur++;
        } else if (arr[cur] < pivot) {
            // cur要后移，因为交换上来的新值肯定<=pivot值
            swap(arr, ++less, cur++);
        } else {
            // 注意这里cur不用移动，因为交换上来的新值不知道其大小
            swap(arr, --more, cur);
        }
    }
    swap(arr, more, right);
    return new int[]{less + 1, more};
}

快排的时间复杂度是$O(nlogn)$，额外空间复杂度是 $O(logn)$ 。关于空间消耗，其实就是左右两边一直往下划分两半，所以就是二叉树的深度 $logn$.