论文阅读：Disentangling User Interest and Conformity for Recommendation with Causal Embedding

发表于 更新于

WWW’21 , DICE模型

Abstract

造成用户从众行为的潜在原因有很多，我们需要把用户真实兴趣与从众因素解耦，所以提出了DICE模型，它可以嵌入于各种 backbone 推荐方法。我们分别为用户和物品分配兴趣和盲从性的embeddings，并利用训练数据达到只让embedding捕捉一种特征的效果。

Introduction

之前的模型是从物品角度出发，去解决物品的流行度偏差，我们则从用户角度出发，分离用户的兴趣和盲从因素。做解耦的好处是：

  1. Robustness，解决了训练和测试数据的OOD问题
  2. Interpretability，解耦当然更有利于理解用户在推荐系统中真正的偏好和其受到的影响

Motivation

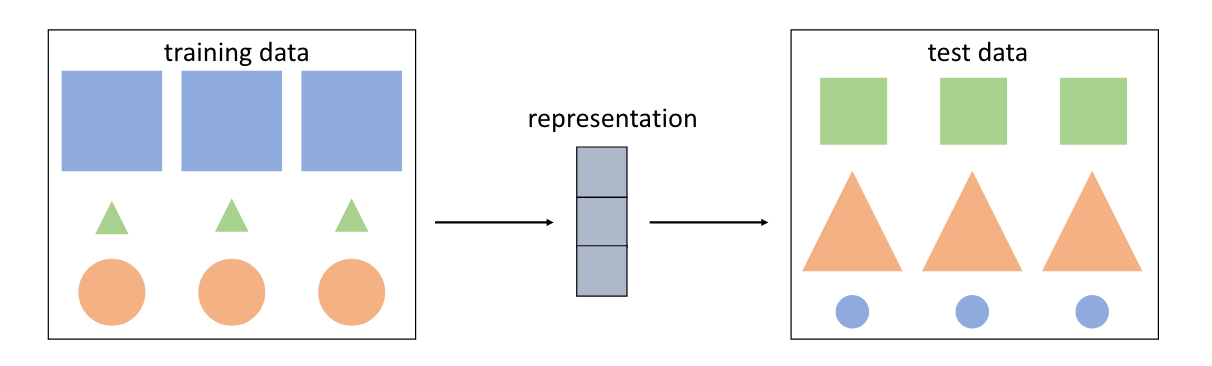
比如我们的任务是形状的检测，但由于模型训练数据的问题，算法可能会以为正方形都具有蓝色、面积大的特征；而三角形都具有绿色、面积小的特征。如果测试数据和训练数据是独立同分布（IID）的，那算法就会学到错误的关于形状的特征。我们强制让训练集和测试集不同分布，这样提高模型鲁棒性。

其实这也是对比学习要解决的问题

实际上我们的不同分布是指训练集和测试集的 item popularity 的分布不同

Model

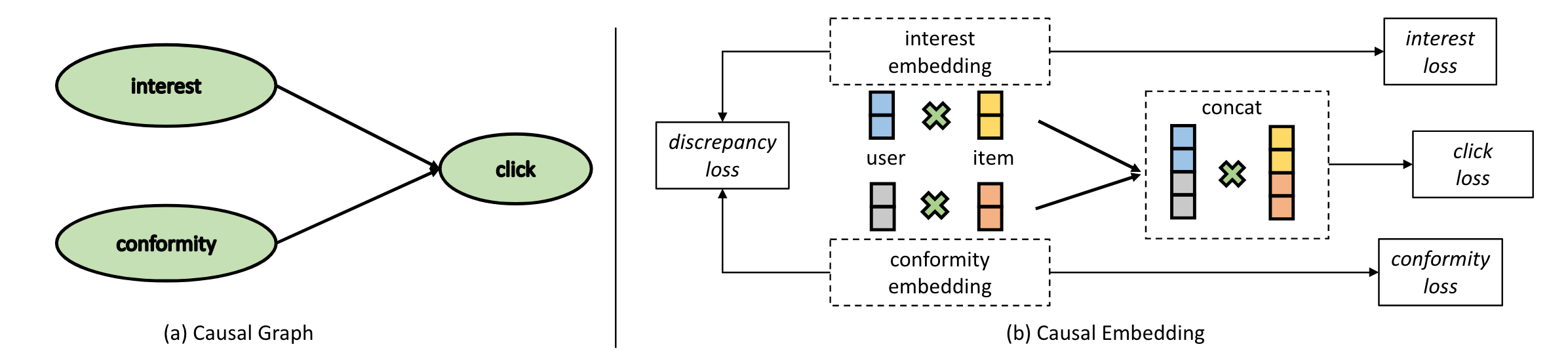
Causal Embedding

从因果图出发，建立兴趣与从众性的模型：

就表示 matching score。这里用加法建模有过去文献的支撑，不用乘法是因为给定 exposed items 时，用户的盲从性依然会起作用，导致无法解耦 ❓ 当然，这里只建模了两种因素，本模型很容易扩展到多个因素。

SCM模型：

其中的 具体分别定义如下：



表示向量内积。这里用户应该有 interest 和 conformity 的 embeddings，而物品应该有表示 characteristic 和 popularity 的 embeddings，这里为了方便把物品的embeddings也分别叫做interest和conformity。

为什么不用乘法用加法，我理解的是乘法模型中，四个向量被乘到一起去了，没有完全分离，加法运算在梯度更新参数的时候会解耦一点。

Disentangled Representation Learning

Mining Cause-specific Data

上面的加法等式方程无法解出 和 ，所以我们需要挖掘出单一因素的数据来训练模型，但是我们现在只有混合各类因素的观测数据。

结合因果图，上面的三个节点形成了 collider 结构，其中 interest 节点和 conformity 节点是相互独立的，但是如果我们对 click 节点施加干预（使其不变），那上面两个节点就是相互关联的了。我们分别用 和 矩阵表示兴趣和盲从的评分矩阵。

从两方面考虑：

  1. 用户与物品 a 产生交互，没有和物品 b 交互，而且物品 a 流行度高于物品 b，我们就有以下的不等式：

  2. 用户与物品 c 产生交互，没有交互物品 d，但物品 d 流行度高于物品 c，我们得到结论：

我们把数据 划分成:

  • ：负样本（没有交互的物品）流行度低于正样本
  • ：负样本流行度高于正样本

分别对应了上面的两个方面。现在，我们的方程就是可解的了。

建模的时候用 表示用户的正例和负例

Conformity Modeling


怎么理解两个式子。第一个式子是针对 ，正例的流行度是高于负例的，所以就是正的BPR；第二是针对 ，正例的流行度低于负例，所以取负号。

Interest Modeling

这里只有 没有 ， 因为在 里面我们只能确定 conformity 的大小关系，无法确定 interest；但是在 里面，流行度低的反而被用户选择，流行度高的没有被选择，有力地证明了这其中用户的兴趣起到了决定作用，对于正例物品 i 的兴趣绝对高于负例 j，所以就是这样的loss

Estimating Clicks


这个损失函数就不分数据集了，是一个总体交互的体现。

Discrepancy Task

此外，对于所有用户和物品的 embeddings，用 和 表示，我们定义三个任务，分别是最大化两者的 L1,L2和 距离。

关于 可以看论文：https://arxiv.org/pdf/1010.0297.pdf

Multi-task Curriculum Learning

同时训练上述四个损失函数：

从上面的公式我们可以看到，如果两个物品的流行度差距比较大，也就是 和 的差距大，那么不等式就有较高的置信度。所以我们要拉远正负例子之间的流行度差距，采用了一种 Popularity based Negative Sampling with Margin (PNSM) 方法提高了算法的置信度。

如果一个物品的流行度是 ，那么我们采样的时候会采集流行度大于 或者小于 的物品，其中的 和 都是 margin 值。

结合课程学习，如果 margin 值比较大，那么不等式的置信度也大，那么这些task就比较容易，那么在上面的损失函数中，我们也设置较大的 权重；我们减小 margin 值后也相应减小 。通过课程学习，我们着重在高置信度的样本上进行了优化，所以解耦的效果也就更好了。

Experiment

如何获得 intervened data？采样的时候，越是流行度高的（出现次数多的），我采样比例就相应减少（类似 inverse popularity），这样可以达到测试和训练数据非独立同分布的效果。

源码：https://github.com/tsinghua-fib-lab/DICE

RQ1 Performance

  • 我们的模型分数最高，耶✌🏻

  • 我们的模型可以被轻松集成到其他基础推荐模型中，耶✌🏻

  • 其他模型在不同数据集和metrics上表现时好时坏，唔😢

相比较在一个用户 embedding 上加一个标量表示用户偏好产生的偏差，我们的模型则有更强的表达力，效果也最好。

RQ2 Interpretability and Robustness

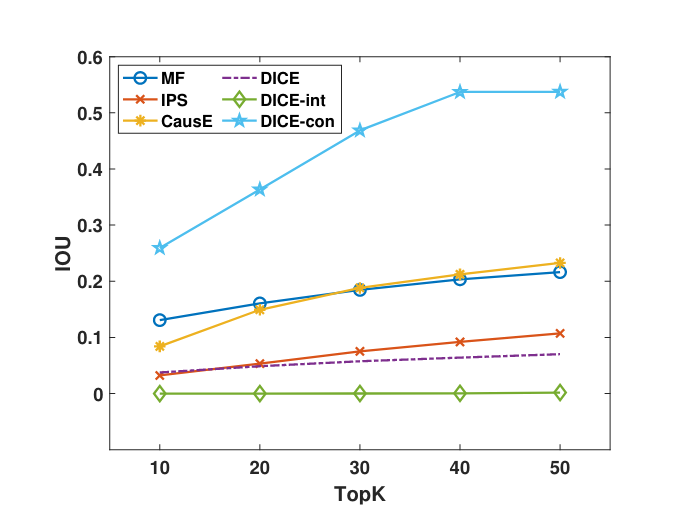
其中IOU代表在多大程度上推荐流行的物品。我们发现DICE-con就是越流行的越可能推荐，而DICE则是效果更好的。

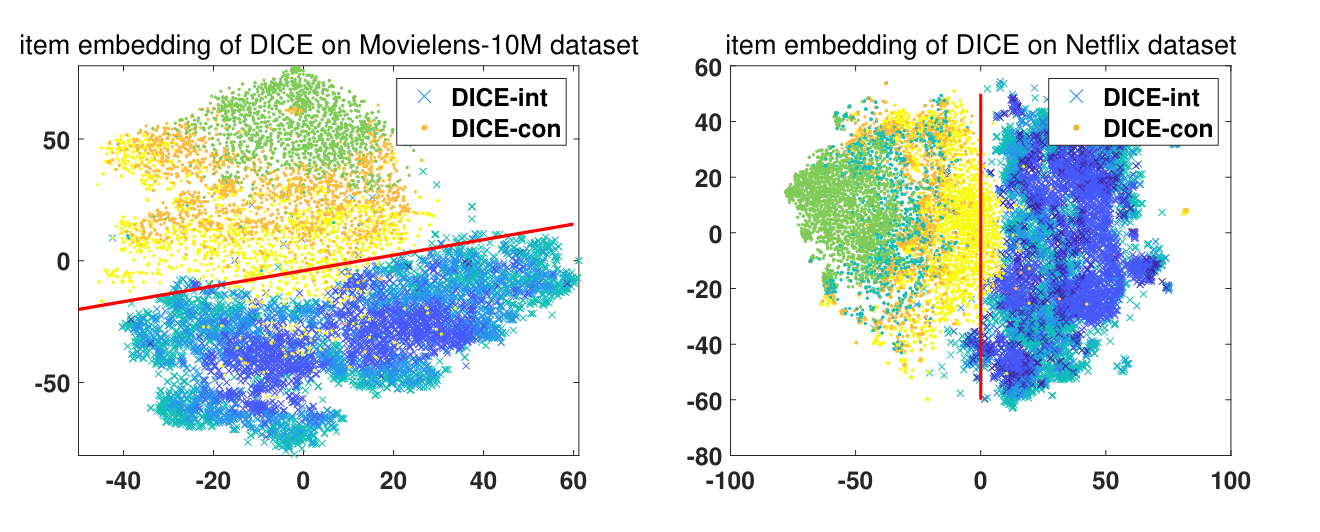
解耦两个embedding的可视化效果，也非常不错。

RQ3 Ablation Study

分别验证了PNSM、Conformity 建模部分、课程学习、Discrepancy Loss四个部分

RQ4 Proportion of Intervened Data

Intervened Data 在训练集占比越大，那么模型受到OOD问题的影响就会比较小，结果鲁棒性就好。本实验就为了求证，在 Intervened Data 占比不同的情况下，模型效果是否出色。

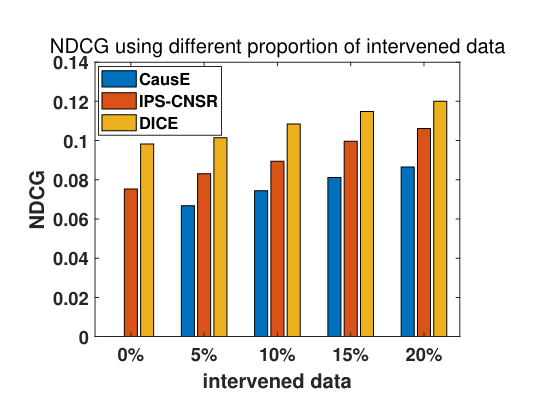
如图，在 Intervened Data 占比很小的时候模型性能依然出色。