两个单链表相交的相关问题

发表于 更新于

来看一道有关链表的题目：

给定两个单链表的头结点 head1 和 head2，这两个链表可能相交，也可能不相交。请实现一个函数，若两链表相交，则返回相交的第一个结点；若不相交，则返回 null。
进阶要求：如果链表1的长度为 N，链表2的长度为 M，时间复杂度请达到 *O(N+M)*，额外空间复杂度请达到 *O(1)*。

如上所示，根据题意可以立刻画出一个单链表相交的示意图。

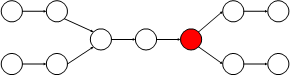
这里需要注意，不可能画出如下所示的相交示意图，因为此题规定了单链表，而如下图所示的链表中必有一个结点（图中用红色标出）拥有两条指针，这违反了单链表的定义。这里也可以得到一个重要结论：两条链表的尾结点一定是相同的。

那么根据第一张图的情况，如何求得相交的第一个节点呢？

第一个思路：将第一个链表的结点插入一个 HashSet 中，再将第二个链表结点插入，若插入过程中函数返回 false，则两个链表有相交，立刻返回此时的结点。这种思路极易想到，但它不满足空间复杂度的进阶要求。

第二个思路也比较好理解：让两个指针分别遍历一遍两个链表，得到两个链表的长度，将其相减，得到它们的差，设为 L。然后两个指针回到起点，较长的那个链表上的指针先走 L 步，接下来两个指针一起走，那么最后指针相遇的地方就是相交的第一个结点了。这个算法只用了常数个变量，空间复杂度达到 *O(1)*。

对应代码稍微花点时间，也能实现出来，但是真的就这一种情况吗？

其实这道题隐藏着一个陷阱：单链表可能存在环。因为环的存在，上述算法的第一步就执行不下去了，两个指针会在环内不停转圈。所以这道题必须分情况讨论。

既然考虑环，先来想想，一个链表有环，一个链表无环，它们可以相交吗？答案是否定的，还是受限于“单链表只有一个指针”的性质，我们无法画出这样的相交示意图来。

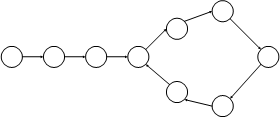
那么，只可能是两个链表都有环，于是画出下面这两张示意图。

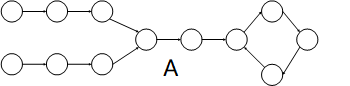
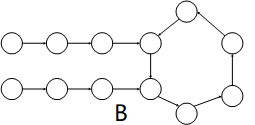
接下来需要区分一下这两种情况。可以发现：A 情况中两条链表由一个结点进环，而 B 情况的两条链表是分别进环的。于是我们在设计整个算法时，不仅仅要判断题目给出的两个链表是否有环，还要知道链表进环的第一个结点是什么。

于是我们设计一个 getLoopNode() 函数，当链表无环时，返回 null，否则返回进环的第一个结点。

首先要判断单链表有环，这是一个经典的题目，它的思路是：设置一个快指针和一个慢指针，快指针每次走两步，慢指针每次走一步，若快慢指针最终相遇，则链表有环，否则无环。就像以前数学课做的追及问题一样，跑道上有两个人同时在跑步，一个速度快，一个速度慢，跑得快的人总会追上慢的人。放在这里，链表中存在的环就是一个环绕操场的跑道，快慢指针总会在环中相遇。

接着来求进环的第一个结点。方法是：快慢指针相遇后，快指针回到自己链表的起点，和慢指针一起走，且两者每次都只走一步。当两个指针再次相遇时，相遇处就是环的第一个结点。

这个方法和它的结论似乎不可思议，我们用纯粹简单的数学证明一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
设一个单链表环外有 x (x∈N)个结点，环内有 y (y∈N*)个结点；
快指针一次走两步，慢指针一次走一步，假设它们共同走了 k 步后相遇，
此时快指针在环内走了 2k-x 步，慢指针在环内走了 k-x 步；
既然它们可以相遇，那么必然有 (2k-x) mod y = (k-x) mod y；
我们计算一下 2k-x 和 k-x 的差值，它一定是 y 的倍数，得到 k = ny(n∈N*)。

快指针回到它的起点，再走到环的第一个结点，需要走 x+1 步，
从快指针从起点出发到环的第一个结点，慢指针走了 (k-x) mod y + x + 1 步，
那它就是在环内的第 [(k-x) mod y + x + 1] mod y 个结点处。

设 k-x 和 y 相除的商是 A，余数是 a；
设 (k-x) mod y + x + 1 和 y 相除的商是 B，余数是 b；
有：Ay + a = k - x，By + b = a + x + 1；
余数 b = a + x + 1 - By = (n - A - B)y + 1。
一个数除以 y 的余数是 y 的整数倍再加上 1，很明显，n - A - B = 0。

所以，慢指针此时在环的第一个结点处。

思路和其原理都清楚了，我们就可以实现 getLoopNode() 函数了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private static Node getLoopNode(Node head) {
		if (head == null || head.next == null || head.next.next == null) {
			return null;
		}
		// 快指针
		Node n1 = head.next;
        	// 慢指针
		Node n2 = head.next.next;
		while (n1 != n2) {
			if (n2.next == null || n2.next.next == null) {
				return null;
			}
			n2 = n2.next.next;
			n1 = n1.next;
		}
        	// 快指针从头开始
		n2 = head;
		while (n1 != n2) {
            		// 不相遇，则双方每次走一步
			n1 = n1.next;
			n2 = n2.next;
		}
		return n1;
	}

两个链表调用一下上述的函数，得到两个结果 loop1 和 loop2，分别表示两个链表的环的第一个结点。

如果 loop1 和 loop2 都非空且相等，那么就对应情况 A。之前两个链表都无环的那种算法里，两个指针一起遍历到链表末尾停止才得到两个链表的长度，那这里只需要相应让两个指针遍历到 loop1（或者loop2），获得环前两个链表的长度，一样可以求得两个链表进环的第一个结点。

如果 loop1 和 loop2 都非空但是不等，那么除了情况 B 之外，这两个链表也有可能完全不相交，各自分离，如下所示。

那么假设一个指针从 loop1 开始走，在它再次走到 loop1 之前，若遇到了 loop2 ，那么这两个链表是相交的，返回结果 loop1 或者 loop2 都可以；若该指针没有遇到 loop2 ，那么两链表相离。

上述过程的代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
private static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {
		Node cur1 = null;
		Node cur2 = null;
		if (loop1 == loop2) {
            		// 情况 A
			cur1 = head1;
			cur2 = head2;
			int n = 0;
			while (cur1 != loop1) {
				n++;
				cur1 = cur1.next;
			}
			while (cur2 != loop2) {
				n--;
				cur2 = cur2.next;
			}
            		// 较长链表的指针
			cur1 = n > 0 ? head1 : head2;
            		// 较短链表的指针
			cur2 = cur1 == head1 ? head2 : head1;
			n = Math.abs(n);
			while (n != 0) {
				n--;
				cur1 = cur1.next;
			}
			while (cur1 != cur2) {
				cur1 = cur1.next;
				cur2 = cur2.next;
			}
			return cur1;
		} else {
			cur1 = loop1.next;
			while (cur1 != loop1) {
				if (cur1 == loop2) {
                    			// 可以遇到 loop2，属于情况 B
					return loop1;
				}
				cur1 = cur1.next;
			}
			return null;
		}
	}

解决此问题，千万不要想当然，而是要考虑多种情况，设计不同的算法。当然这其中也需要一定的经验积累。