题目内容
题目链接:N皇后 & N皇后 II
GitHub 导航:https://github.com/Avicii4/LeetCode/tree/master/problems/Math/N-Queens
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。如下图。
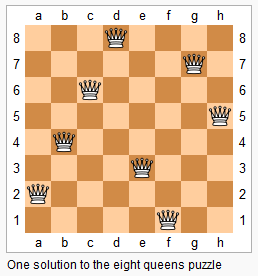
在国际象棋中,皇后可以说是移动最“自由”的棋子了,若无阻挡,她可以到达同一行、同一列或同一斜线方向上的任何一个位置。所以,题目中要求的“不能相互攻击”就是要让这些棋子不能同处一行、一列或一斜线上。
“N皇后”要求给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
而“N皇后 II”题目给定一个整数 n,返回 n 皇后不同的解决方案的数量。
所以两道问题的设定没有变,可以一起解决。
思路分析
这道题的基本思路是回溯法,这也是在 LeetCode 中比较常用的算法了。接下来描述一下本题的思路:
- 算法开始, 清空棋盘,当前行设为第一行,当前列设为第一列;
- 在当前行,当前列的位置上判断是否满足条件,若不满足,跳到第4步;
- 在当前位置上满足条件的情形:
(1) 在当前位置放一个皇后,若当前行是最后一行,记录一个解;
(2) 若当前行不是最后一行,当前行设为下一行, 当前列设为当前行的第一个待测位置;
(3) 若当前行是最后一行,当前列不是最后一列,当前列设为下一列;
(4) 若当前行是最后一行,当前列是最后一列,回溯,即清空当前行及以下各行的棋盘,然后,当前行设为上一行,当前列设为当前行的下一个待测位置;
(5)以上返回到第2步;
- 在当前位置上不满足条件的情形:
(1) 若当前列不是最后一列,当前列设为下一列,返回到第2步;
(2) 若当前列是最后一列了,回溯,即,若当前行已经是第一行了,算法退出,否则,清空当前行及以下各行的棋盘,然后,当前行设为上一行,当前列设为当前行的下一个待测位置,返回到第2步。
有了这个算法思路,接下来进行代码的编写。本来我考虑用二维数组存储每个棋子的位置坐标,这样也是大部分人第一时间想到的存储结构。不过,也可以用一个一维数组 location[i] 来存储位置信息,其中 i 是棋子所在的行数,location[i] 是棋子所在的列数。
再来看看怎么判断是位置否符合条件。一维数组每个位置代表一行,那么棋子在同一行的冲突情况肯定不会发生了;同一列方向上,检查数组中有没有其他地方与 location[i]的值一样;至于斜线方向,联系几何坐标系的内容,很容易知道两个位置的行数之差和列数之差的绝对值相等,则这两个棋子在同一斜线上。根据这个想法,写出方法 isAttackable()。
1
2
3
4
5
6
7
| private static boolean isAttackable(int row, int[] location) {
for (int i = 0; i < row; i++) {
if (location[row] == location[i] || Math.abs(location[row] - location[i]) == row - i)
return true;
}
return false;
}
|
接下来的回溯过程用递归来实现,虽然损失了一定的效率,但简单易懂。递归的过程在完整代码中有所体现。
程序代码
N皇后
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| class NQueens {
public List<List<String>> solveNQueens(int n) {
int[] location = new int[n];
List<List<String>> res = new ArrayList<>();
insertQueen(n, 0, location, res);
return res;
}
private static void insertQueen(int n, int row, int[] location, List<List<String>> res) {
if (row == n) {
List<String> arrayList = new ArrayList<>();
for (int i = 0; i < n; i++) {
StringBuffer sb = new StringBuffer();
for (int j = 0; j < n; j++) {
if (j == location[i]) {
sb.append("Q");
} else {
sb.append(".");
}
}
arrayList.add(sb.toString());
}
res.add(arrayList);
return;
}
for (int i = 0; i < n; i++) {
location[row] = i;
if (!isAttackable(row, location)) {
insertQueen(n, row + 1, location, res);
}
}
}
private static boolean isAttackable(int row, int[] location) {
for (int i = 0; i < row; i++) {
if (location[row] == location[i] || Math.abs(location[row] - location[i]) == row - i)
return true;
}
return false;
}
}
|
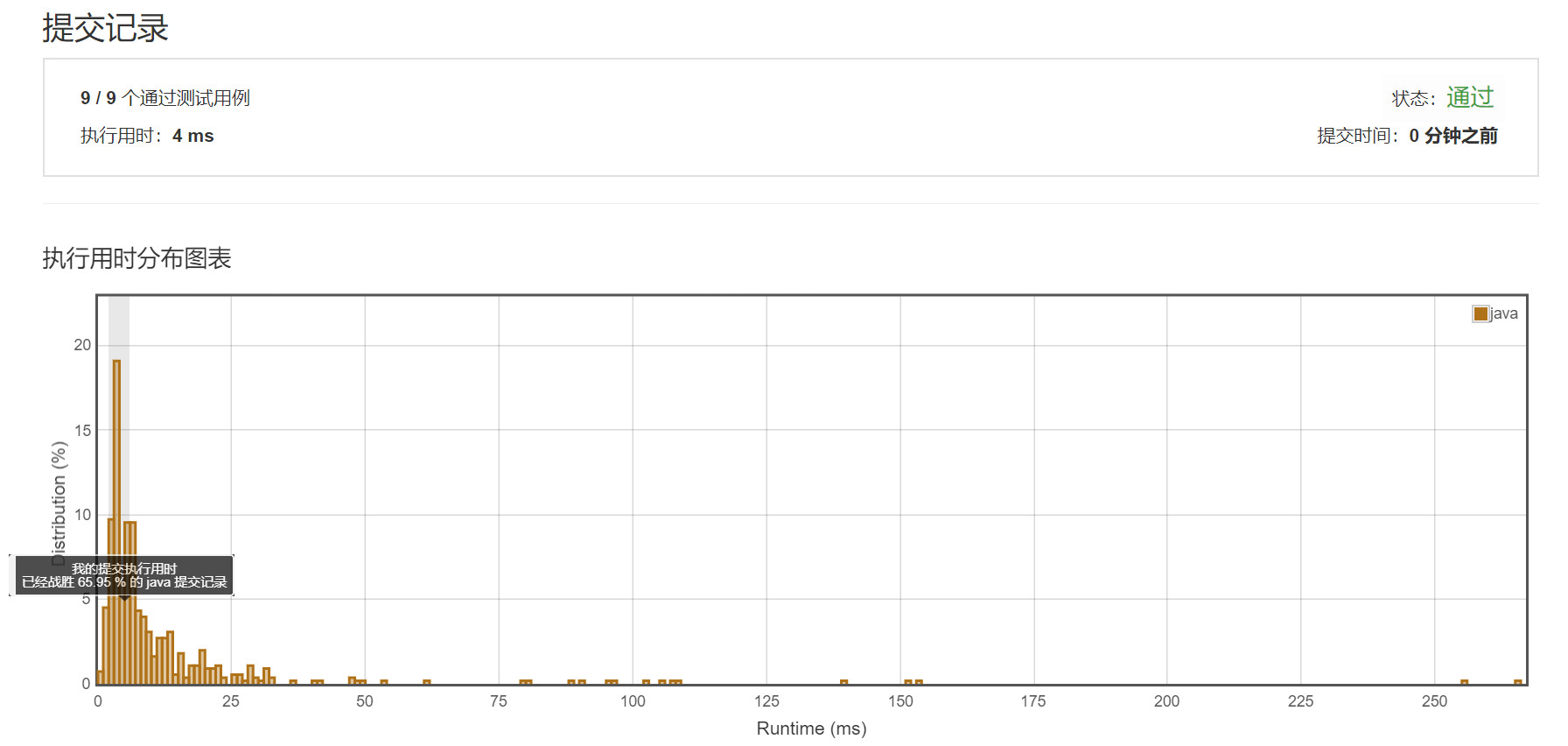
提交结果:
N皇后II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class NQueensII {
public int count = 0;
public int totalNQueens(int n) {
if (n <= 0) {
return 0;
}
check(0, new int[n]);
return count;
}
private void check(int row, int[] location) {
if (row == location.length) {
count++;
return;
}
for (int i = 0; i < location.length; i++) {
location[row] = i;
if (!isAttackable(row, location)) {
check(row + 1, location);
}
}
}
private static boolean isAttackable(int row, int[] location) {
for (int i = 0; i < row; i++) {
if (location[row] == location[i] || Math.abs(location[row] - location[i]) == row - i)
return true;
}
return false;
}
}
|
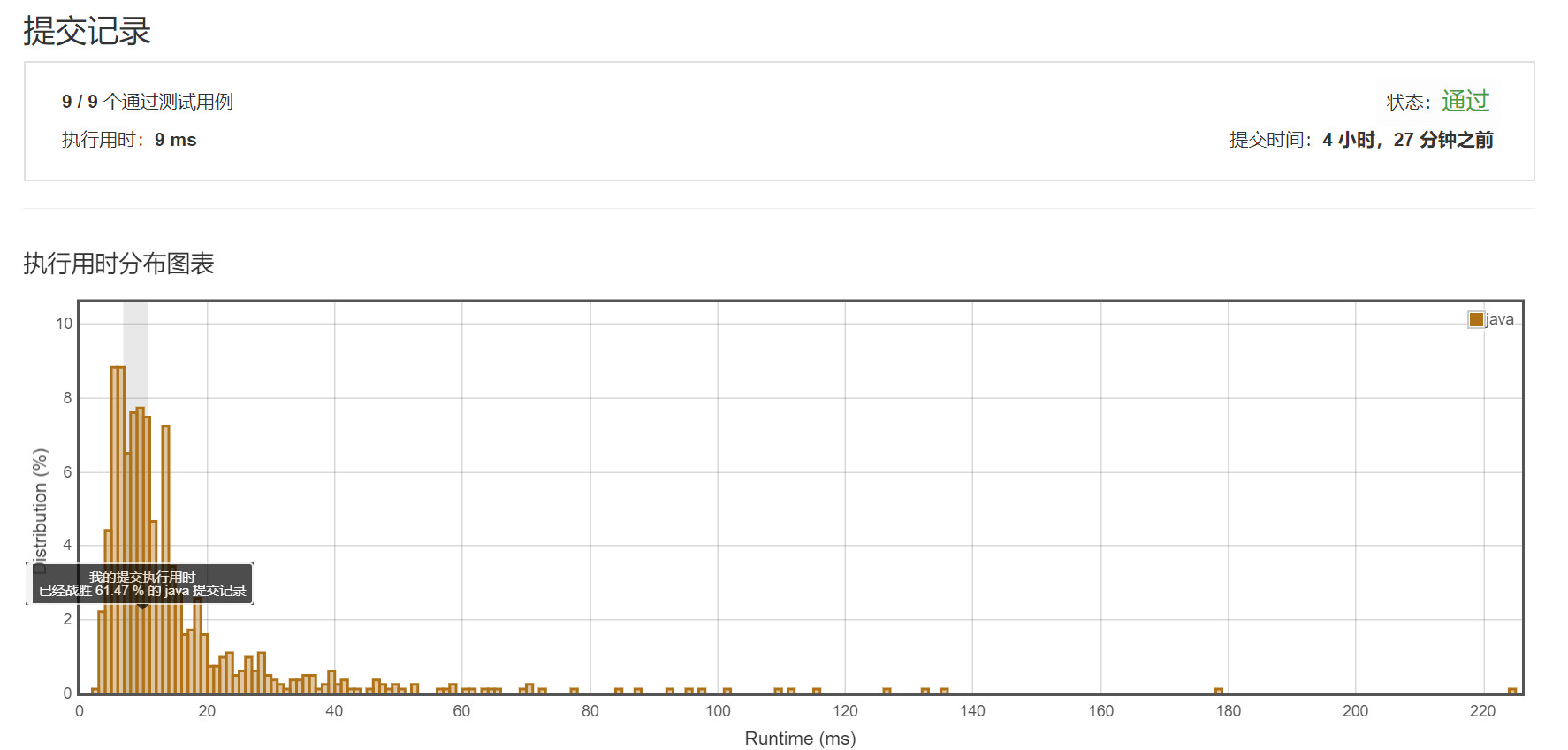
提交结果 :