LeetCode 15：3Sum

发表于 更新于

题目内容

题目链接 ：三数之和
GitHub 导航：https://github.com/Avicii4/LeetCode/tree/master/problems/Array/3Sum
给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。
注意：答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，满足要求的三元组集合为：

1
2
3
4
[
  [-1, 0, 1],
  [-1, -1, 2]
]

思路分析

首先映入脑海的方法就是三重循环，把所有三数的组合取出来一一判断，但很明显这种方法的时间复杂度达到了可怕的 O(n3) ，定会报出超时错误，故不采用。
慢慢摸索其他解法。本题要求结果不含重复的元素，且每个三元组中的元素是升序排列的，故先将数组 nums 排序，方便排除重复项。接下来利用双指针法的思想，首先在头尾两个地方设置指针 i 和 k 并固定，再在中间设置一个变量 j ，移动寻找符合条件的数组元素。也就是设置变量 i 从头开始向后走，设置变量 k 从尾开始向前走，在它们中间找出符合的 j 值。示意图如下所示：

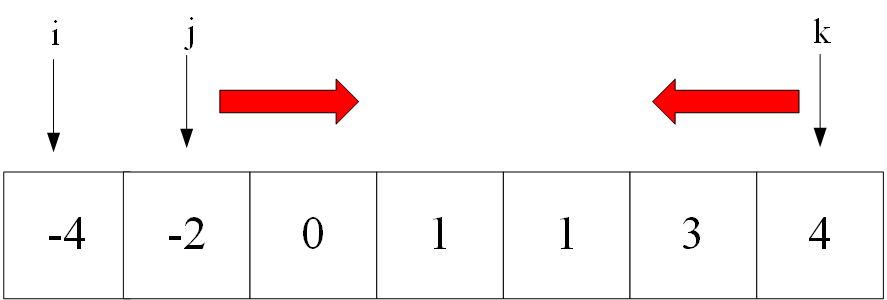
注意，循环过程中始终要保证这三个变量的相对位置不变，保证结果的正确性。
接下来考虑代码的优化。之前我们对数组进行了排序，若数组中有重复元素，应该立刻跳过，避免结果中出现重复项。变量 i 作为最外层循环，若 nums[i] == nums[i - 1] ，则可以直接 continue 跳过此次循环；对于变量 j 和 k，可以写出如下的代码：

1
2
3
4
while (j < k && nums[j] == nums[j + 1])
    j++;
while (k > j && nums[k] == nums[k - 1])
    k--;

还有什么地方能优化？本题要求三数之和为0，如果和大于0，那么三数必定偏大，由于数组已经被置为升序，程序也就没有必要再向后寻找了；同样地，假如和为负数，三数必定偏小，因此：

1
2
if (sum > 0)  k--;
else          j++;

程序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class ThreeSum {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> result = new ArrayList();
        if (nums.length < 3)
            return result;
        for (int i = 0; i < nums.length; i++) {
            if (i > 0 && nums[i] == nums[i - 1])
                continue;
            int j = i + 1;
            int k = nums.length - 1;
            while (j < k) {
                int sum = nums[i] + nums[j] + nums[k];
                if (sum == 0) {
                    List<Integer> elem = Arrays.asList(nums[i], nums[k], nums[j]);
                    result.add(elem);
                    while (j < k && nums[j] == nums[j + 1])
                        j++;
                    while (k > j && nums[k] == nums[k - 1])
                        k--;
                    j++;
                    k--;
                } else if (sum > 0)
                    k--;
                else
                    j++;
            }
        }
        return result;
    }
}

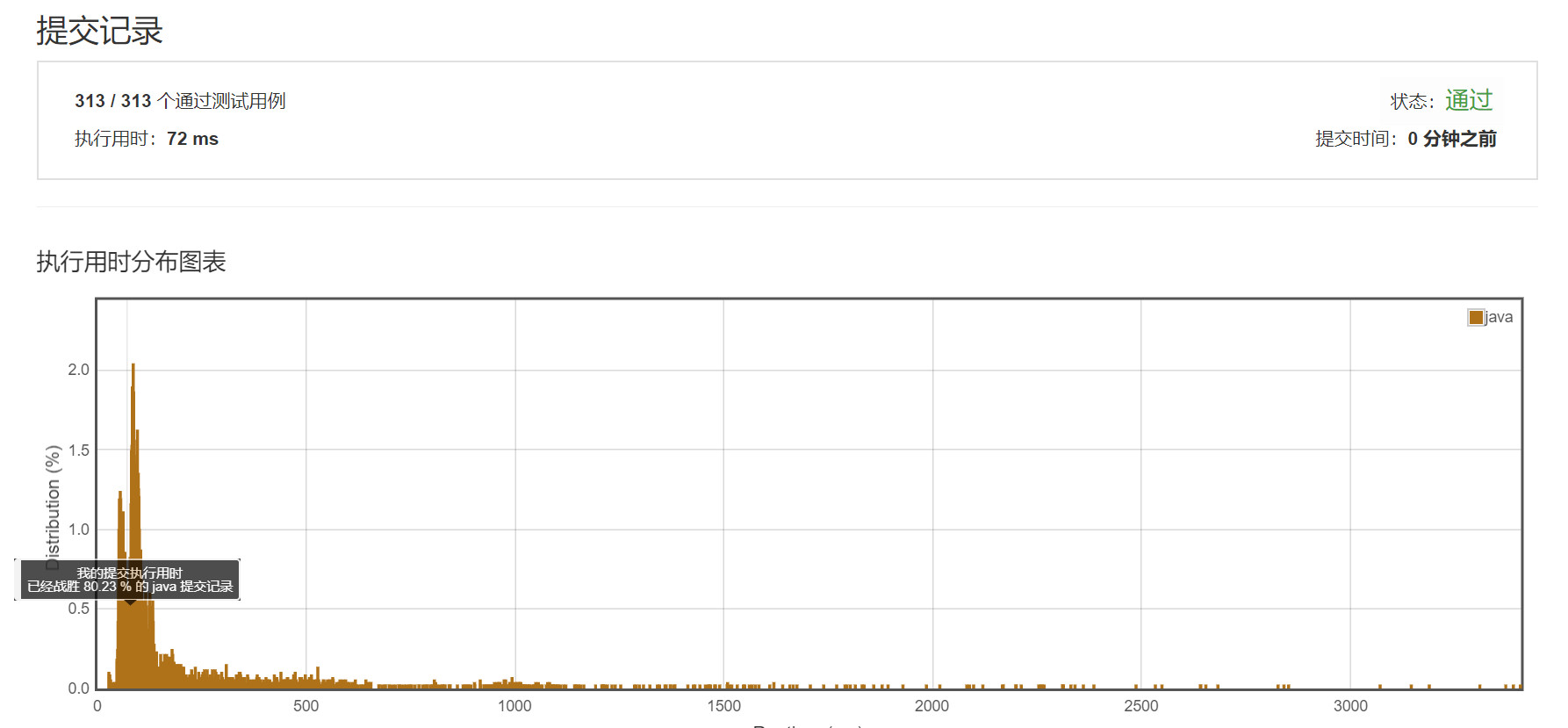
提交结果：